Non-linear least squares

The non-linear least squares problem is

$$\begin{equation}\label{Non-linearleastsquares_prob} \min_{\vx\in\R^n} \frac{1}{2}\|r(\vx)\|_2^2, \end{equation}$$

where $r:\R^n→\R^m$ is the residual vector. The $i$th component of residual vector is $r_{i}(\vx):\R^n→\R$. The non-linear least squares problem reduces to the linear least squares problem if $r$ is affine, i.e. $r(\vx) = \mA\vx-\vb$.

Example: Position estimation from ranges

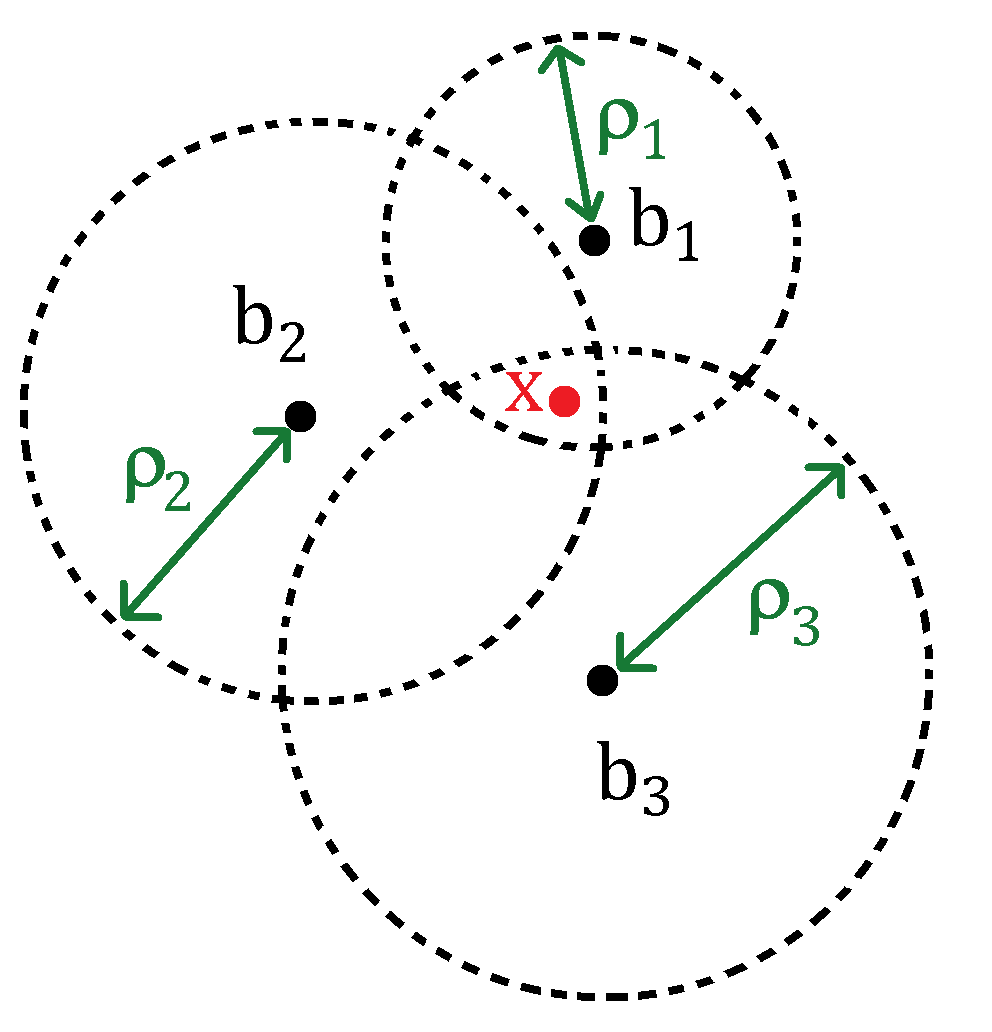
Let $\vx \in \R^2$ be an unknown vector. Fix $m$ beacon positions $\vb_{i} \in \R^2,\ i = 1,\dots,m$. Suppose we have noisy measurements $\vrho \in \R^m$ of $2$-norm distance between a becon $\vb_{i}$ and the unknown signal $\vx$, i.e.

$$ ρ_{i} = |\vx- \vb|_2 + ν_i \quad \text{for } i=1,\dots,m. $$ Here, $\vnu \in \R^m$ is noise/measurement error vector. The position estimation from ranges problem is to estimate $\vx$ given $\vrho$ and $\vb_i, \ i = 1,\dots, m$.

A natural approach to solve this problem is by finding $\vx$ that minimizes $\sum_{i=1}^m(ρ_{i} - \|\vx- \vb\|_2)^2$. Define $r_i(\vx) := ρ_{i} - \|\vx- \vb\|_2$. Then we can estimmate $\vx$ by solving the non-linear least squares problem

$$\min_{\vx\in \R^n} \frac{1}{2}\|r(\vx)\|_2^2.$$

In contrast to linear least squares program, the non-linear least squares program generally contain both global and local minimizers. We can will use the following approach to find a minimizer of NLLS.

---

Gauss-Newton method for NLLS

Given starting guess $\vx^{(0)}$
Repeat until covergence:

1. linearize $r(x)$ near current guess $\bar{\vx} = \vx^{k}$
2. solve a linear least squares problem to get the next guess $\vx^{k+1}$,

---

Linearization of residual

We can solve non-linear least squares problem \eqref{Non-linearleastsquares_prob} by solving a sequence of linear least squares problem. These linear least squares subproblem results from linearization of $r(\vx)$ at current estimate of the ground truth $\vx$.

The linear approximation of $r(\vx)$ at a point $\bar{\vx} \in \R^n$ is

$$r(\vx) = \bmat r_1(\vx)\\\vdots\\ r_n(\vx)\emat \approx \bmat r_1(\bar{\vx}) +\nabla r_1(\bar{\vx})\trans(\vx - \bar{\vx}) \\ \vdots \\ r_m(\bar{\vx}) +\nabla r_m(\bar{\vx})\trans(\vx - \bar{\vx}) \emat = A(\bar{\vx}) \vx -b(\bar{\vx}),$$

where $A(\bar{\vx})\in\R^{m\times n}$ is the Jacobian of the mappring $r(x)$ at $\bar{\vx}$ and $b(\bar{\vx}) = A(\bar{\vx})\vx - r(\bar{\vx}) \in \R^m$. The Jacobian of $r(x)$ at $\bar{\vx}$ is

$$A(\bar{\vx}) = \bmat \nabla r_1(\bar{\vx})\trans\\ \vdots \\ \nabla r_m(\bar{\vx})\trans\emat.$$

We get the following minimization program after replacing $r(\vx)$ with its linear approximation at $\vx^{(k)}$:

$$\vx^{(k+1)} = \mathop{\text{argmin}}_{\vx\in\R^n} \|A(\vx^{(k)})\vx - b(\vx^{(k)})\|_2^2.$$

Starting at a current estimate $\vx^{(k)}$, we can determine the $\vx^{(k+1)}$ by solving the above linear least squares program.

Dampening

For ease of exposition, let

$$\bar{\mA} = A(\vx^{(k)}), \quad \bar{\vb} = b(\vx^{(k)}), \text{ and } \bar{\vr} = r(\vx^{(k)}).$$

We assume that $\bar{\mA}$ is full rank. Consider

$$\begin{align*} \vx^{(k+1)} = &\mathop{\text{argmin}}_{\vx\in\R^n} \|\bar{\mA}\vx - \bar{\vb}\|_2^2\\ =& (\bar{\mA}\trans\bar{\mA})^{-1}\bar{\mA}\trans\bar{\vb}\\ =& (\bar{\mA}\trans\bar{\mA})^{-1}\bar{\mA}\trans(\bar{\mA}\vx^{(k)} - \bar{\vr})\\ = &\vx^{(k)} - (\bar{\mA}\trans\bar{\mA})^{-1}\bar{\mA}\trans\bar{\vr} \end{align*}$$

Here, $\vx^{(k+1)}$ is the $k+1$ Gauss-Newton estimate. Note that $(\bar{\mA}\trans\bar{\mA})^{-1}\bar{\mA}\trans\bar{\vr}$ solves $\min_{\vx\in\R^n} \|\bar{\mA}\vx - \bar{\vr}\|_2^2$. Let

$$\vz^{(k)} = \mathop{\text{argmin}}_{\vx\in\R^n} \|\bar{\mA}\vx - \bar{\vr}\|_2^2.$$

The dampened Gauss-Newton step is

$$\vx^{(k+1)} = \vx^{(k)} - \alpha \vz^{(k)},$$

where $\alpha \in (0,1]$.

---

Dampened Gauss-Newton method for NLLS

Given starting guess $\vx^{(0)}$
Repeat until covergence:

1. linearize $r(x)$ near current guess $\bar{\vx} = \vx^{k}$:
   $\quad r(\vx) \approx r(\bar{\vx}) - A(\bar{\vx})(\vx-\bar{\vx})$
2. solve a linear least squares problem:
   $\quad \vz^{(k)} = \mathop{\text{argmin}}_{\vx\in\R^n}\|A(\bar{\vx})\vx - r(\bar{\vx})\|_2^2$
3. take damped step:
   $\quad \vx^{(k+1)} = \vx^{(k)} - \alpha^{(k)}\vz^{(k)}, \quad 0<\alpha^{(k)}\leq 1$

until converged

---