QR factorization

Orthogonal and orthonormal vectors

Let $\vx, \vy\in\R^n$ be any two vectors. By cosine identity, we have

$$\vx\trans\vy = \|\vx\|_2\|\vy\|_2\cos(\theta)$$

where, $\theta$ is the angle between $\vx$ and $\vy$. So, $\vx$ and $\vy$ are orthogonal ($\theta = 0$), if $\vx\trans\vy = 0$. Furthermore, we say $\vx$ and $\vy$ are orthonomal if $\vx$ and $\vy$ have unit 2-norm and are orthogonal, i.e.

$$\vx\trans\vy = 0, \quad \vx\trans\vx =1 , \quad \vy\trans\vy = 1.$$

Orthogonal matrices

A matrix $\mQ$ is orthogonal if it is square and its columns are all pairwise orthogonal. For an orthogonal matrix $\mQ = \bmat\vq_1 &\dots&\vq_n\emat$, we have

$$\mQ\trans\mQ = \mQ\mQ\trans = \mI.$$

Since, a matrix $\mB$ is the inverse of a matrix $\mA$ if $\mB\mA =\mA\mB = \mI$, the inverse of an orthognal matrix is its transpose, i.e.

$$\mQ^{-1} = \mQ\trans.$$

Orthogonal matrices have many good properties. One such property is that inner products are invariant under orthogonal transfromations. So, for any vectors $\vx,\ \vy$, we have

$$(\mQ\vx)\trans(\mQ\vy) = \vx\trans\mQ\trans\mQ\vy = \vx\trans\vy.$$

This also implies that 2-norm is invariant to orthogonal transformations as $\|\mQ\vx\|_2 = \|\vx\|_2$. Another property of othogonal matrices is that their determinant is either $1$ or $-1$. This can be observed from the fact that for a matrix $\mA$ and $\mB$, we have $\det(\mA\mB) = \det(\mA)\det(\mB)$ and $\det(\mA)= \det(\mA\trans)$. So, from $\mQ\trans\mQ = \mI$, we get

$$\det(\mQ\trans\mQ) = \det(\mI) \iff \det(\mQ)^2 = 1 \iff \det(\mQ) = ±1.$$

QR factorization

Let $\mA \in \R^{m\times n}$. A factorization of $\mA$ with

$$\mA = \mQ \mR$$

where $\mQ\in\R^{m\times m}$ is an orthogonal matrix and $\mR \in \R^{m\times n}$ is an upper triangular matrix is called a $QR$ factorization of $\mA$. In the case with $m\geq n$ and $\rank(\mA) = k \leq n$, the $QR$ facorization will have the following shape:

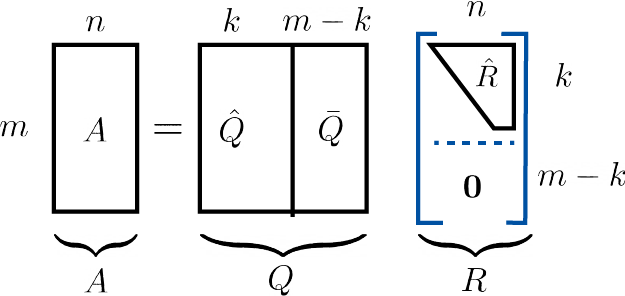
In the above figure,

1. $\mQ$ is an orthogonal matrix.
2. $\mR$ is a upper triangular matrix, i.e. $R_{ij}=0$ whenever $i>j$.
3. $\hat{\mQ}$ spans the range of $\mA$.
4. $\bar{\mQ}$ spans the nullspace of $\mA\trans$.

In Julia, we can compute the QR decompisition of a matrix using:

m = 4
n = 3
A = randn(m,n)
F = qr(A)

Let $\mQ = \bmat \vq_1 \dots \vq_m \emat$. We can express the columns of $\mA$ as

$$\begin{align*} \va_{1} &= r_{11} \vq_{1}\\ \va_{2} &= r_{12} \vq_{1}+r_{22}\vq_2\\ &\vdots\\ \va_{n} &= r_{1n} \vq_{1} + r_{2n}\vq_2+\dots+r_{kn}\vq_{k}\\ \end{align*}$$

So, we can compactly write the matrix $\mA$ as $\mA = \hat{\mQ}\hat{\mR}$. This is the reduced (thin or economode) QR factorization of $\mA$. In the case when $m\geq n$ and $\mA$ is full rank, we get following figure:

Solving least squares via QR

The $QR$ factorization can be used to solve the least squares problem

$$\min_{\vx \in\R^n}\frac{1}{2}\|\mA\vx-\vb\|_2^2,$$

where $\mA \in \R^{m\times n}$ and $\vb\in \R^m$. We consider the case where $m\geq n$, but QR factorization can be used to solve the other case as well. Consider

$$\begin{align*} \|\mA\vx-\vb\|_2^2 &= (\mA\vx-\vb)\trans(\mA\vx-\vb)\\ &= (\mA\vx-\vb)\trans\mQ\mQ\trans(\mA\vx-\vb)\\ & = \|\mQ\trans(\mA\vx-\vb)\|_2^2\\ &=\left\|\bmat\hat{\mR}\\\vzero\emat\vx-\bmat\hat{\mQ}\trans\\\bar{\mQ}\trans\emat\vb\right\|_2^2\\ & = \|\hat{\mR}\vx - \hat{\mQ}\trans\vb\|_2^2+\|\bar{\mQ}\trans\vb\|_2^2 \end{align*}$$

So, minimizing $\|\hat{\mR}\vx - \hat{\mQ}\trans\vb\|_2^2$ will minimize $\frac{1}{2}\|\mA\vx-\vb\|_2$. In the case $\mA$ is full rank, we get an invertible $\hat{\mR}$ and the least squares solution which satisfies

$$\begin{equation}\label{QR_leastsquares} \hat{\mR}\vx = \hat{\mQ}\trans\vb, \end{equation}$$

will be unique. In the case when $\mA$ is not full rank, there will be a infinitely many solutions to the least squares problem. For both cases, we can find a least squares solution by solving \eqref{QR_leastsquares} via back substitution.

The figure below shows the geometric prespective of using a QR factorization to solve the least squares problem.

For every $\vb \in \R^m$, $\hat{\mQ}\hat{\mQ}\trans\vb$ is the orthogonal projection of $\vb$ onto the $\range(\hat{\mQ}) = \range(\mA)$. The least squares solution finds a point $\vx$ such that $\mA\vx$ is equal tothe orthogonal projection of $\vb$ onto the $\range(\mA)$. So, we get $\mA\vx = \hat{\mQ}\hat{\mQ}\trans\vb$, which simplifies to \eqref{QR_leastsquares}.